Rainbow Science: How Rainbows Form and How to Find Them

How Rainbows Form and How to Find Them

Archway to the Light

Double Rainbow arch with anti-crepuscular rays converging towards the Sangre de Cristo Mountains north of Santa Fe, New Mexico. This double rainbow shows Alexander’s Dark Band in between the rainbows.

The Recipe For a Rainbow

When direct sunlight illuminates raindrops, a rainbow forms.

However, we rarely see rainbows! This is because a rainbow can only be seen at a well-defined angle -requiring us to be at the right location and time.

The “rainbow angle,” 42 degrees for the primary rainbow, is determined by the physics of how light refracts and reflects inside a raindrop.

The secondary rainbow has an angle of 51 degrees.

You can only see a rainbow when raindrops fall in the direction of 42 degrees from your shadow, and the sun’s elevation is less than 42 degrees above the horizon (unless you are in an airplane or on a mountain top)

When the sun’s elevation is higher than 42 degrees, the rainbow is out of sight below the horizon.

The lower the elevation of the sun, the taller the rainbow.

Ingredients

Falling rain, water spray, or virga
- The falling rain must be along a cone of 42 degrees measured from the shadow of your head
Sun lower than 42 degrees elevation
- Your shadow is longer than your height
Direct sunlight shining on the falling raindrops
- No clouds for fog between the sun and the raindrops
Spread both your hands out as wide as possible with the tips of both thumbs touching each other. In Spanish culture, this would be two cuartas. Now outstretch your arms and put the tip of one of your small fingers (“pinky finger”) on the shadow of your head, the rainbow will found along an arc defined by the pinky finger on your other hand.

A good rule of thumb to determine if the sun is low enough in the sky to see a rainbow is to check if your shadow is longer than your height.

At high latitudes in the Northern Hemisphere summer, the sun elevation stays low in the sky all day and never sets below the horizon for points above the arctic circle. I love it when I spend my summers in Alaska; I frequently see rainbows last for hours. Double rainbow at 10:24 PM, June 25, 2018, sun elevation = 6.0 deg, (latitude = 58.5 deg. N) Katmai National Park & Preserve, Alaska.

The Role of Refraction in Rainbows

A ray of sunlight bends as it enters a raindrop, due to refraction.

Refraction occurs when light travels from one medium into another.

The amount that light bends during refraction depends on the difference in the index of refraction of the media, the angle of incidence of the light, and the wavelength (color)f of the light.

$RefractionDiagram$

When light encounters an interface between two different mediums, it refracts (bends). Some light also reflects from the surface of the interface. The amount of light that reflects from, or refracts through, the interface depends on the angle of incidence of the light, the indices of refraction of the media on both sides of the interface, and on the wavelength (color) of the light.

How a Raindrop Forms a Rainbow

Rays of light from the Sun are redirected in many different directions by raindrops.

Some rays reflect off the surface a raindrop (ray 1′ in the adjoining figure).

Other rays enter the raindrop and are subsequently bent from refraction. These internal rays of light can then exit the other side of the raindrop (ray 2′) or “bounce around” inside the raindrop via internal reflections (ray 3 and ray 4).

When the light ray reaches, an interface between water and air reflection and refraction occurs.

A rainbow is formed from certain light rays concentrated in angle upon exit from the raindrop and redirected towards our eyes.

Not all light rays that interact with raindrops form rainbows. As we will see below, certain light rays are concentrated and redirected towards our eyes — the “rainbow angle” light rays.

Light rays can be redirected in many ways by raindrops. This ray-tracing diagram shows rays reflecting off the exterior of a raindrop and rays refracting across the air-water interfaces and reflecting off the inner surfaces of a raindrop. Rainbows are formed from light rays that follow a special path in raindrops (not shown in this figure).

The physics of reflection, refraction, and dispersion are all involved in forming a rainbow.

With the sun behind us and raindrops in front of us, light rays can reflect from the inside of raindrops back towards our eyes.

At each air-water interface of the raindrop, some light reflects away from the raindrop, and some light enters or leaves the raindrop.

These light rays refract as they enter the raindrop and when they exit the raindrop. Inside the raindrop, the colors of white sunlight separate due to dispersion.

The light rays that form the primary rainbow go through two refractions and one internal reflection (from the rear surface of the raindrop).

Ray diagram of light in raindrop for primary rainbow

The light rays that are responsible for the primary rainbow are diagrammed here. The physics of reflection, refraction, and dispersion are all involved in forming a rainbow. At each air-water interface of the raindrop, some light reflects away from the raindrop, and some light enters or leaves the raindrop. Light refracts (bends) when it enters or leaves the raindrop. The light rays that form the primary rainbow go through two refractions and one internal reflection (from the rear surface of the raindrop).

Angular Concentration of Light Rays – Why a Rainbow is Bright

In 1637 René Déscartes was able to explain the shape of the primary and double rainbow were caused by refraction and reflection in spherical raindrops.

In the laboratory, Déscartes produced rainbows by passing light through a large water-filled flask (to function as a large “raindrop”).

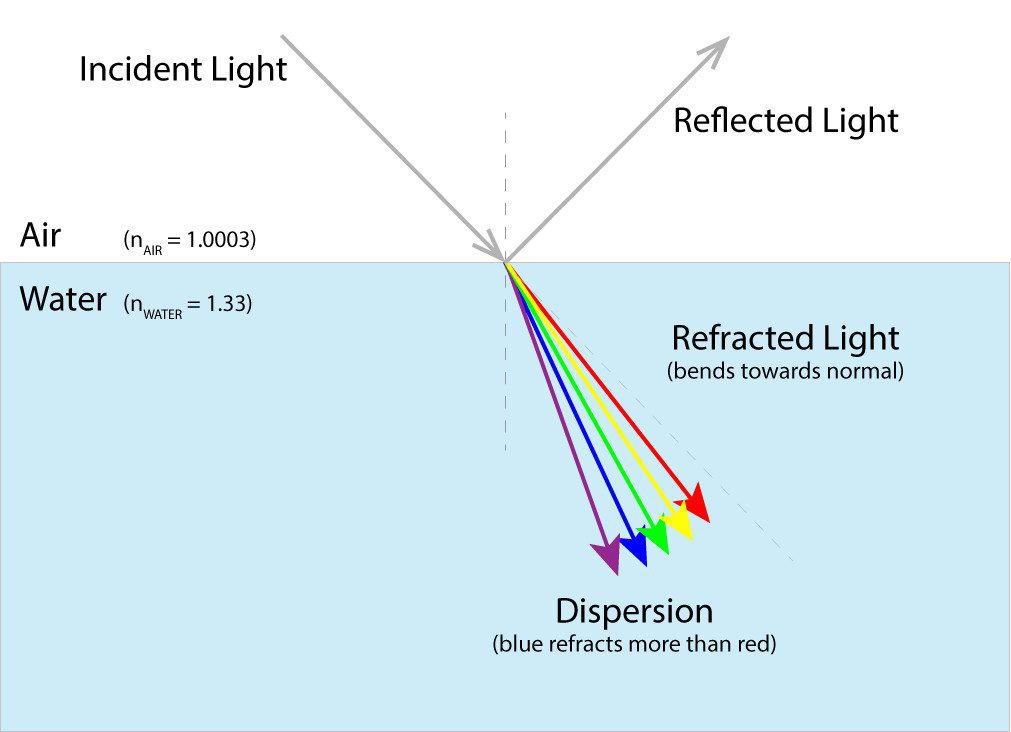
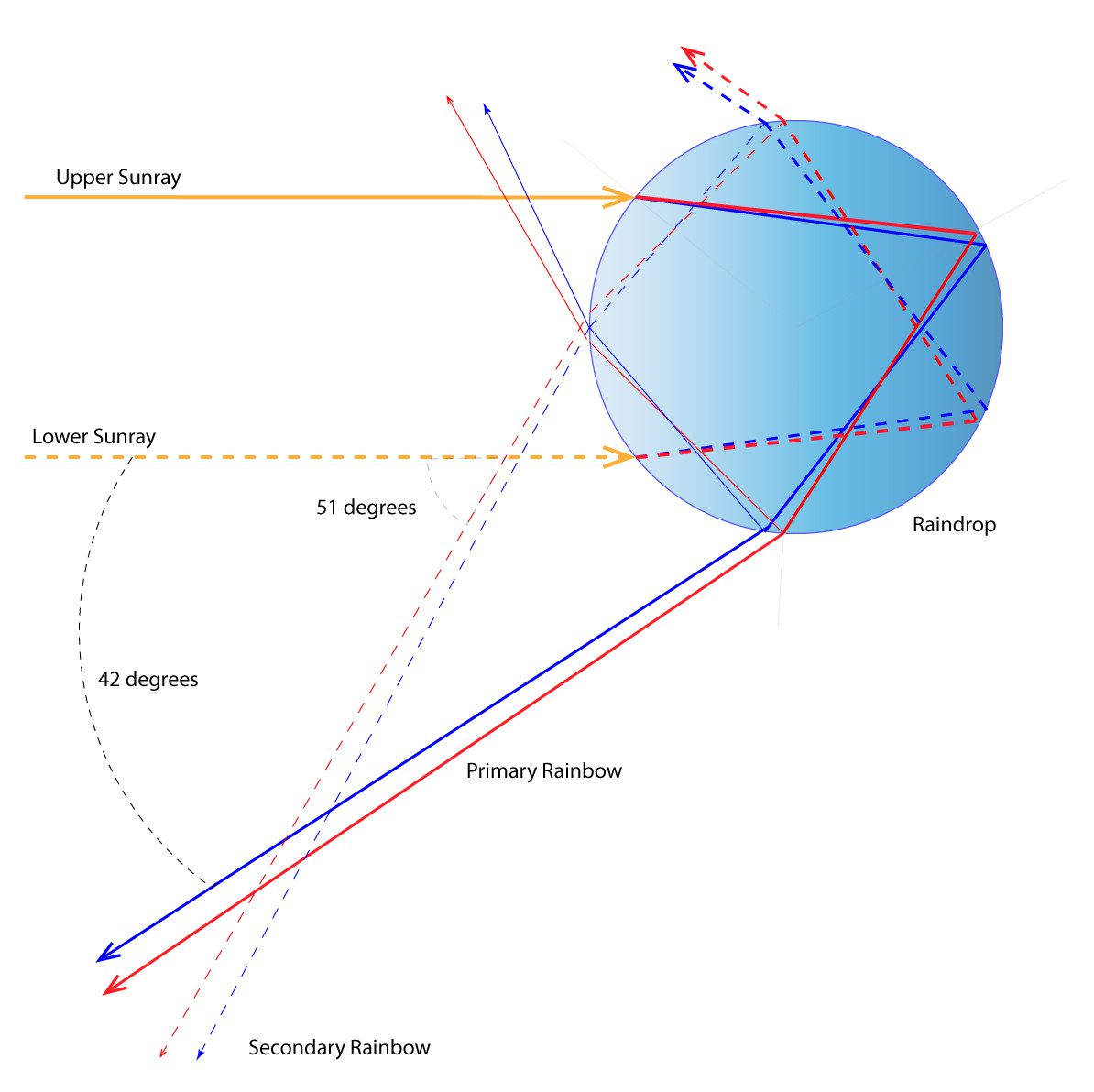
Déscartes applied the laws of reflection and refraction, formulated 16 years earlier by a Dutch scientist, Willebrord Snellius, known as Snell’s Law, to trace light rays through a water drop and correctly calculate the angles for the primary and secondary rainbow.

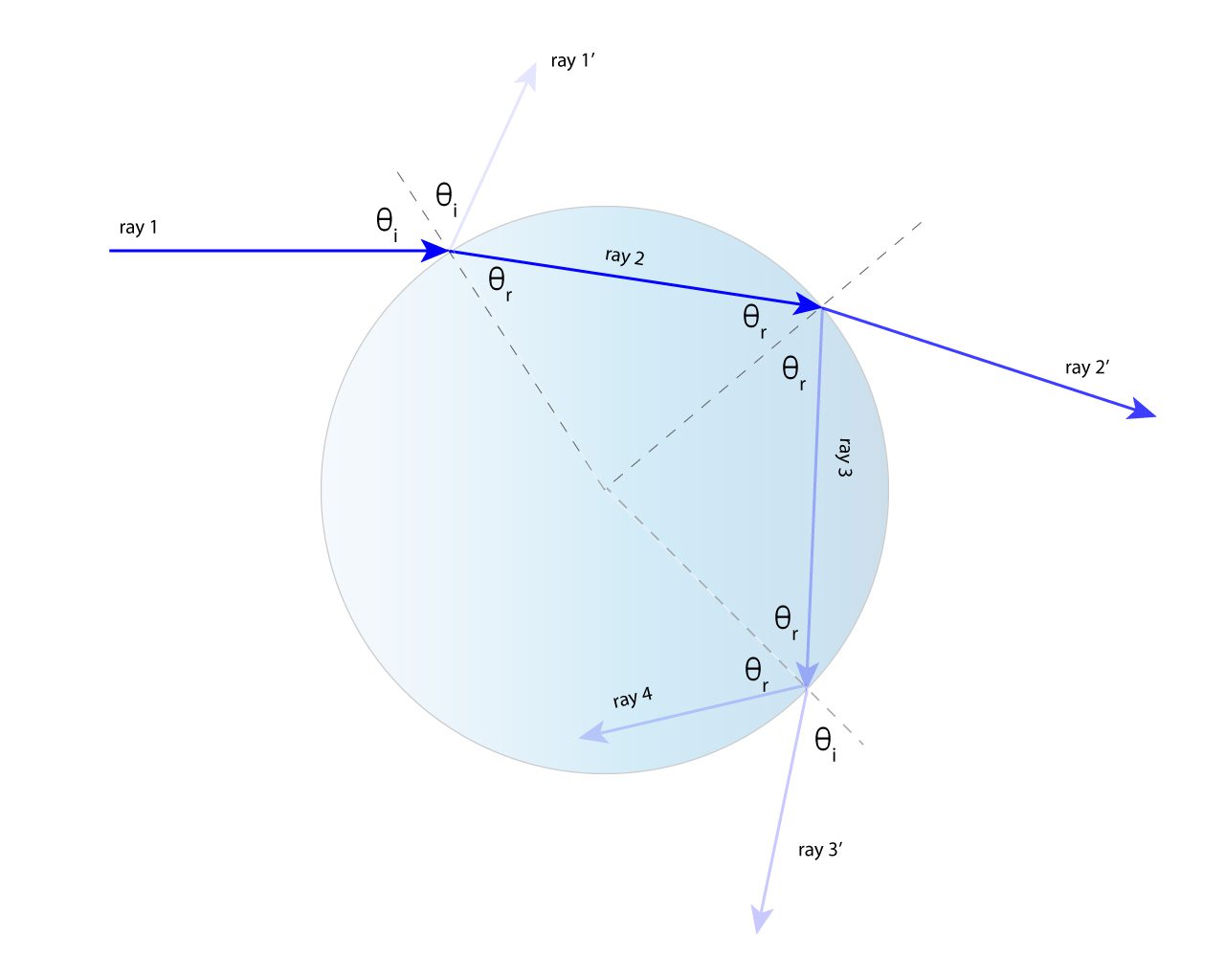
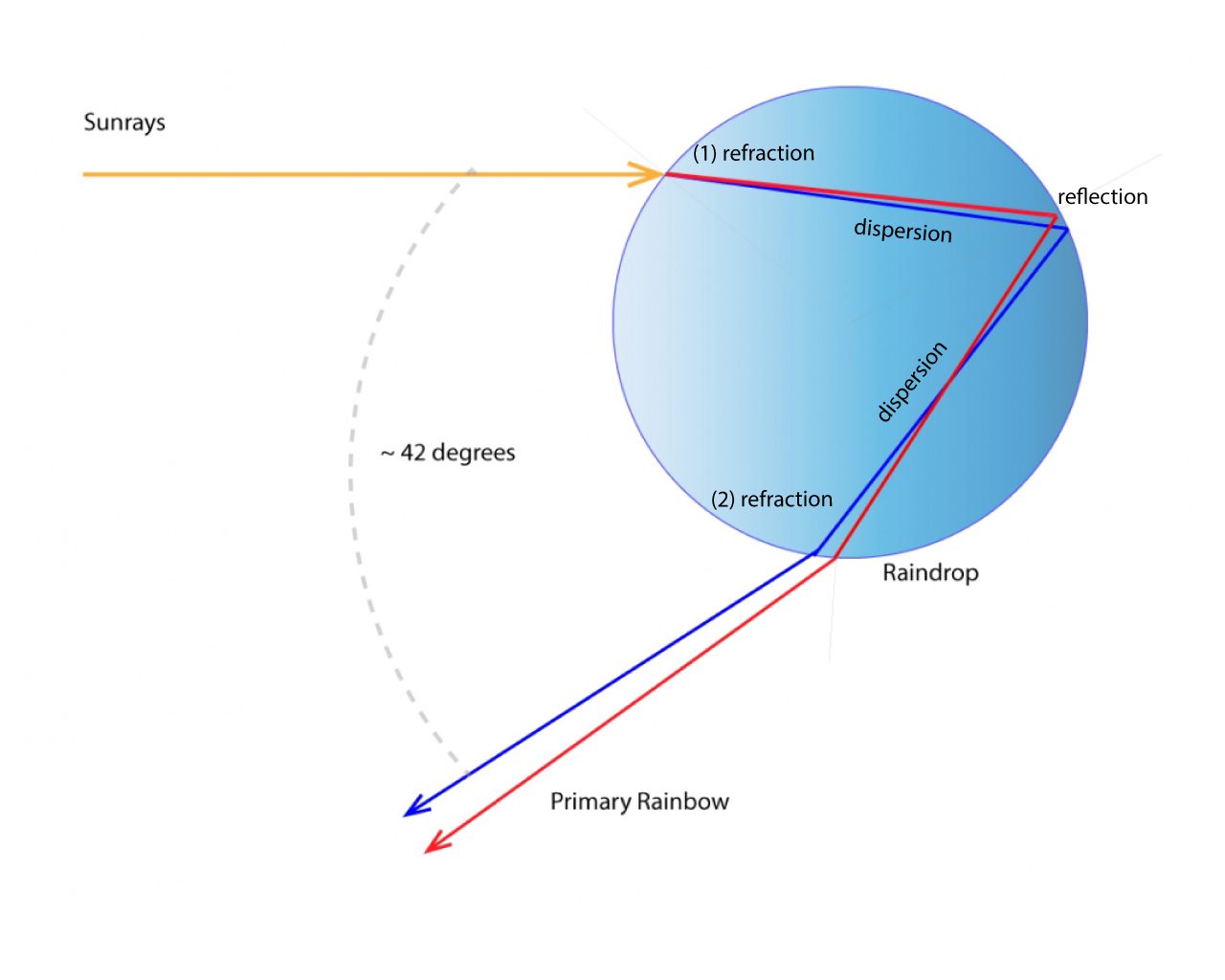
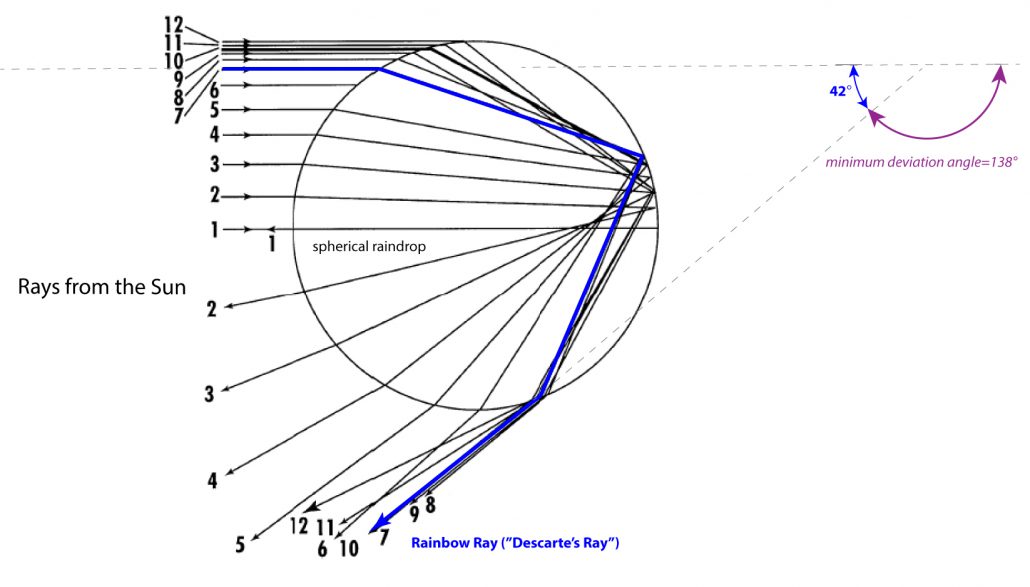
Déscartes was able to show a concentration of light rays around the minimum angle of deviation of the light rays. Light rays that refract twice (once upon entry into the raindrop and once upon exit of the raindrop) and reflect once off the interior back surface of the raindrop are deviated from their original direction. The angle of deviation depends on the distance from the centerline of the raindrop – known as the “impact parameter.”

Light rays that fall perpendicular to the surface of the raindrop, impact parameter = 0, reflect backward with a deviation angle of 180°.

Light rays that hit the raindrop further from the centerline/axis deviate less than 180°. As the impact parameter distance increases, the deviation angle decreases to a minimum value of 138° (for yellow light). This minimum deviation angle corresponds to Ray 7 in the adjacent ray-tracing diagram. As seen from the ray-tracing diagram, there is a concentration of light rays around this minimum deviation angle.

The concentration of light rays around this minimum deviation angle causes the brightness of the primary rainbow that we see — more light is redirected into this angular direction. Different colors have slightly different minimum deviation angles, hence the brightness for each colored arc of the rainbow.

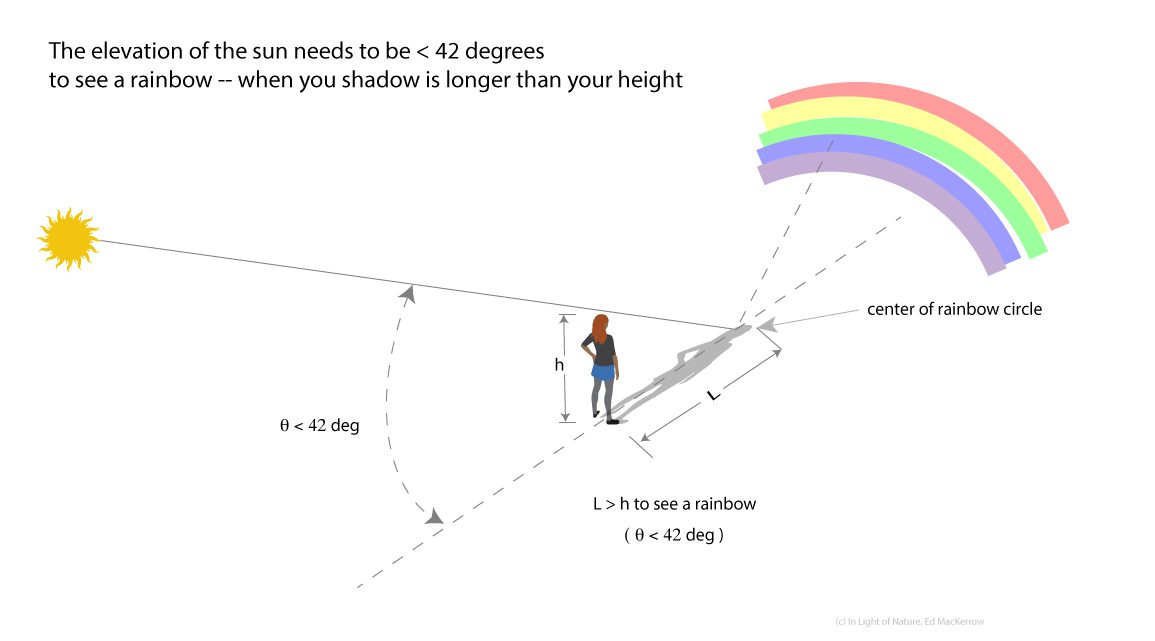
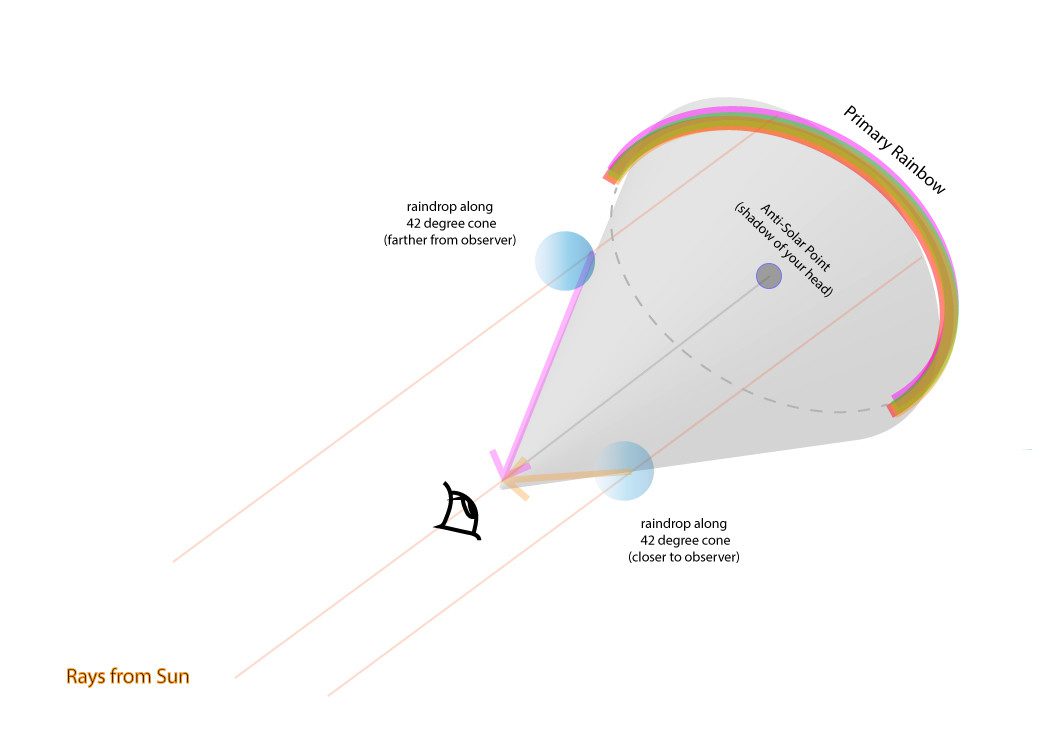
When we transform the minimum deviation angle into the angle we observe the rainbow as measured from the antisolar point (the shadow of our head), we get 180° – 138° = 42°, the “rainbow angle” or “Déscartes Ray.”

Ray diagram for sunlight refracting twice and reflecting once in a raindrop. The exit angles of the rays from the raindrop condense along the minimum deviation angle of 138 degrees. ⁽¹⁾From The mathematical physics of rainbows and glories, John A. Adam, Physics Reports, 356 (2002) 229-365.

The highest angular concentration of light rays (rays 7,8,9 in the above figure) lies at the angle of the “rainbow angle” (42 °), resulting in a brighter light in the rainbow. The light inside in the arc of the primary rainbow (i.e. < 42 °) is brighter than the ambient light due to more light rays being reflected in this direction (rays 10,11, 12 in the ray-tracing diagram), even though they are not as concentrated as the colored rays of the rainbow. In this photograph, the brighter white light can be seen interior to the primary rainbow arc.

The Index of Refraction of Rain Drops

The index of refraction of a given medium equals the speed of light in a vacuum divided by the speed of light inside that medium. Light slows down inside denser media. This means the index of refraction for everything but a vacuum is greater than 1.0.

The index of refraction of air is 1.0003, and 1.33 for water.

In the diagram above, light bends towards the normal⁽²⁾The normal to a surface is a vertical line perpendicular to the surface to the surface (shown by the vertical dashed line) as it enters the water.

The colors of white light separate in the raindrop due to dispersion, resulting from the wavelength dependence for the index of refraction. Blue light refracts more than red.

Inside the raindrop, some light reflects from the rear surface of the raindrop. Some of this reflected light exits the front surface of the raindrop. As this light exits the raindrop, it refracts again since it leaves a denser media (water) into a less dense medium (air) and therefore bends away from the normal to the surface of the raindrop.

Color (wavelength nm)	Red (660 nm)	Orange (610 nm)	Yellow (580 nm)	Green (550 nm)	Blue (470 nm)	Violent (410 nm)
Water	1.331	1.332	1.333	1.335	1.338	1.342

The index of refraction for different wavelengths of light (color) is listed here. Violets and blues have a higher index of refraction than reds, and therefore violet refracts more (bends more) than red.

Dispersion is Why We See the Different Colors in a Rainbow

Why are the colors of sunlight separated in a rainbow?

When light crosses from one medium to another it refracts (bends). The amount of refraction depends on the angle of incidence on the media interface and the wavelength (color) of the light. Shorter wavelengths (purples and blues) refract (bend) more than longer wavelengths (oranges – reds).

Dispersion of the “white light” (all colors) from the sun inside the raindrop separates the colors by angle. This effect accounts for the width of the rainbow with redder colors on the outside of the primary rainbow and blues and purples being on the inside of the bow. Note that different raindrops direct a specific color to our eye (i.e. the red bands of the rainbow and the blue bands of the rainbow originate from different raindrops).

The Double (“Secondary”) Rainbow

Inside the raindrop, some of the light reflected from the back surface reflects one more time from the front inner surface of the raindrop. These light rays then refract as they exit the raindrop towards the observer, with a minimum deviation angle of 231 degrees, which equates to (231 – 180 degrees) = 51 degrees in angular radius from the antisolar point. See the dashed rays in the figure below.

Double rainbow and anticrepuscular rays at sunset in New Mexico

Double rainbow outside of Santa Fe, New Mexico. Anti-crepuscular rays can be seen converging to the anti-solar point. The darker sky between the primary and secondary rainbow is Sir Alexander’s dark band, caused by total internal reflection inside the raindrops.

The light rays that form a double rainbow are shown here by dashed lines. These rays undergo two reflections inside the raindrop before they exit the drop at 51 degrees from the anti-solar point (the shadow of your head). The second reflection reverses the colors in the secondary bow from the order of colors in the primary bow. Note how different rays of sunlight reach our eyes from the primary rainbow and secondary rainbow.

Some exciting things to look for in a double rainbow include:

The dark sky between the primary and secondary rainbow, known as “Alexander’s Dark Band,”
The ordering of colors differs between the two rainbows,
The secondary rainbow is wider than the primary bow.

Light rays that lie between the primary rainbow angle of 42-degrees and the secondary rainbow at 51-degrees cannot be refracted back towards the viewer due to the concept of total internal reflection. These rays cannot make it out of the raindrop. Light propagating from inside a medium with a higher index of refraction to a medium with a lower index of refraction can only make it out of the material for a given range of angles. You can see this effect in double rainbows as the dark band between the two rainbows. The dark area is “Alexander’s Dark Band,” named after the Greek Philosopher Alexander of Aphrodisias, who first described the effect in 200AD.

If you look closely at the above ray-tracing diagram, you can see that different light rays produce the primary and secondary rainbow.

Thinking about the angles involved, you realize that the raindrops which produce the secondary rainbow are different from the raindrops that produce the primary bow. The raindrops responsible for the secondary bow are at an angle of 51-degrees from your shadow, whereas the raindrops associated with the primary bow are at 42 degrees.

A double rainbow showing Alexander’s Dark Band between the primary and secondary rainbows. Note the shadow of my camera on the tripod at the center of the rainbows — my camera is the anti-solar point at the center of the rainbow arc. The colors in the secondary rainbow are reversed from the primary rainbow due to the extra internal reflection inside the raindrop for rays that form the secondary rainbow. The width of the color band in the secondary rainbow is wider than the primary rainbow.

Looking for Rainbows in All the Right Places

To see a rainbow, you need to be standing in the right place, with the sun to your back and the rain falling in a direction along the 42-degree angular radius from the anti-solar point (the shadow of your head on the ground).

Rainbows do not exist at a given location in space. Rainbows appear if you look in the direction of the rainbow angles (42 or 51 degrees). The raindrops causing the rainbow do exist in space at a given location. You can see a rainbow formed by water drops just a few feet in front of your face! This rainbow will look the same as one formed by water drops located miles away.

Once while photographing at Yosemite, I met another photographer who wanted to show me the rainbow from Yosemite Falls as the morning sun was cresting the top of Half Dome. When we first arrived at Yosemite Falls, we did not see any rainbow. Why? There was bright sunlight and plenty of water droplets in the air from the waterfall mist. We were standing in the wrong place. Once we moved to the side, so the falls were at 42-degrees from our shadow, we could see the rainbow!

A Great Time to See a Rainbow

The rainbow at Yosemite Falls disappeared later that morning. Why? There were water droplets in the air and bright sun. As the sun rose in the sky, the rainbow at Yosemite Falls sank towards the ground and then disappeared.

Since the primary rainbow has an angular radius of 42-degrees from the anti-solar point when the elevation of the sun in the sky is higher than 42-degrees the top of the rainbow will be below the horizon, and out of sight.

The sun has to be lower than 42-degrees elevation in the sky to see rainbows. When the sun angle is low, the rainbow is very tall. When the sun is higher in the sky, the rainbow is low in the sky up to the point where you can no longer see it.

When you see a rainbow, raindrops from different parts of the sky are creating the primary rainbow and the secondary rainbow. The primary rainbow forms from raindrops that do not contribute to the secondary rainbow, and vice versa. The rainbows are circular due to the symmetry of the refraction and reflection of light in the raindrops. To see a full rainbow, there must be a broad enough angular region of the sky that has rain and is being illuminated by direct sunlight.

Raindrops anywhere along an angle of 42 degrees between the viewer and their shadow contribute to the primary rainbow they see. The holds for the secondary rainbow at an angle of 51 degrees. It does not matter how close the observer is to the falling rain; all primary rainbows fall along the 42-degree line. You can see this effect by spraying a mist from your garden hose with the sun to your back.

A steam locomotive from the narrow gauge Cumbres & Toltec Scenic Railroad in Chama, New Mexico releases steam, allowing for a rainbow to form at a very close range to me. It is late afternoon and the train is traveling from east to west in this photo, so the sun is to the right.

A primary rainbow formed from the steam locomotive. The water droplets from the steam that is responsible for this rainbow are very close to me, as can be seen by the trees behind the bow. Regardless of how close the water droplets are this rainbow forms at the same angle (42-degrees) as it would if the water droplets were miles away.